Cone Volume Calculator

Cone Volume Calculation

Straight

Truncated

Invalid input
Enter dimensions in mm:
Invalid input
Invalid input
Invalid input
Invalid input
Invalid input
Invalid input
Invalid input
Invalid input
Invalid input

Solution by formula:

Cone volume formula using radius and height:

π - constant equal to (3.14); h - cone height; r - base radius of the cone.

Cone volume formula using height and base area:

h - cone height; S - base area

Truncated cone volume formula using radii and height:

π - constant equal to (3.14); r1 - radius of the top base ; r2 - radius of the bottom base; h - height of the truncated cone.

Information

Mathematics is the universal language underlying science, technology, and construction. It plays an essential role in fields such as engineering, architecture, and design. From early education, students are introduced to numerous mathematical principles and formulas, including the fundamental computation of a cone’s volume. Both right (regular) cones and truncated cones are routinely analyzed in professional construction and engineering practices. Our online tool – a Truncated and Right Cone Volume Calculator – provides fast, accurate, and dependable calculations.

A cone is a three-dimensional geometric solid formed by connecting every ray that emanates from a single point—the apex—to each point on a flat surface called the base. In many contexts, the term “cone” specifically refers to the portion of the object defined by linking the apex with the edge of the base.

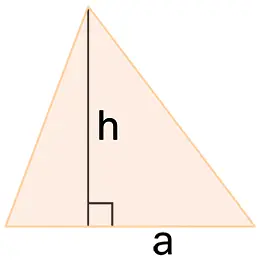
A perpendicular segment drawn from the apex to the base is known as the height of the cone. When the base has a finite area, the cone’s volume is finite and is calculated as one-third of the product of the base area and the height. Therefore, all cones resting on identical bases with equal heights—even when their apexes are located on a plane parallel to the base—have the same volume. When the base is a polygon, the cone becomes a pyramid, categorizing pyramids as a specific type within cones.

A line segment joining the apex to a point on the boundary of the base is referred to as a generator of the cone. Together, these generators form the lateral surface.

In construction and engineering, precision is paramount. Even a minor miscalculation can lead to significant consequences. To ensure both accuracy and efficiency, our online tool is engineered to compute any cone-related parameters by simply entering the essential values into the relevant formula. With this Truncated and Right Cone Volume Calculator, you can quickly determine the volume of a cone in cubic centimeters, cubic meters, or liters.

Three main formulas are used in this calculator:

  1. The formula for calculating the volume of a cone using the radius and height.
  2. The formula that computes the volume based on the base area and height.
  3. The formula for determining the volume of a truncated cone, given its radius and height.

By using our online calculator, you benefit from:

  • Enhanced precision and reliability in the calculated results, minimizing potential errors in professional projects.
  • Significant time savings by eliminating the need for manual computations.
  • An intuitive and user-friendly interface designed for ease of use.

To use our online calculator, follow these steps:

  • Select the type of cone (right or truncated).
  • Enter the initial parameters (height, radius, or base area).
  • After submitting the data, the calculator immediately displays the cone’s volume.

See also: