Oppervlakte driehoek berekenen

Berekenen van de oppervlakte van een driehoek

Formule voor het berekenen van de oppervlakte van een driehoek via 2 zijden en een hoek:

waar a, b — zijden van de driehoek, α — hoek tussen hen.

Formule voor het berekenen van de oppervlakte van een driehoek via de basis en de hoogte:

waar a — basis van de driehoek, h — hoogte van de driehoek.

Formule voor het berekenen van de oppervlakte van een driehoek via de omgeschreven cirkel en zijden:

waar a, b, c — zijden van de driehoek, R — straal van de omgeschreven cirkel.

Formule voor het berekenen van de oppervlakte van een driehoek via de ingeschreven cirkel en zijden:

waar a, b, c — zijden van de driehoek, r — straal van de ingeschreven cirkel.

Formule voor het berekenen van de oppervlakte van een driehoek via een zijde en 2 aangrenzende hoeken:

waar a — zijde van de driehoek, α en β — aangrenzende hoeken, γ — tegenoverliggende hoek, die kan worden berekend met de formule: γ=180—(α+β)

Formule voor het berekenen van de oppervlakte van een driehoek volgens de formule van Heron (als 3 zijden bekend zijn):

waar a, b, c — zijden van de driehoek, p — halve omtrek van de driehoek, die kan worden berekend met de formule p=(a+b+c)/2

Formule voor het berekenen van de oppervlakte van een rechthoekige driehoek via twee zijden:

waar a, b — zijden van de driehoek.

Formule voor het berekenen van de oppervlakte van een rechthoekige driehoek via de hypotenusa en een scherpe hoek:

waar c — hypotenusa van de driehoek, α — een van de aangrenzende scherpe hoeken.

Formule voor het berekenen van de oppervlakte van een rechthoekige driehoek via een rechthoekszijde en een aangrenzende hoek:

waar a — rechthoekszijde van de driehoek, α — aangrenzende hoek.

Formule voor het berekenen van de oppervlakte van een rechthoekige driehoek via de straal van de ingeschreven cirkel en de hypotenusa:

waar c — hypotenusa van de driehoek, r — straal van de ingeschreven cirkel.

Formule voor het berekenen van de oppervlakte van een rechthoekige driehoek via de ingeschreven cirkel:

waar c1 en c2 — delen van de hypotenusa.

De formule van Heron voor een rechthoekige driehoek is als volgt:

waar a, b — rechthoekszijden van de driehoek, p — halve omtrek van de rechthoekige driehoek, berekend met de formule p=(a+b+c)/2

Formule voor het berekenen van de oppervlakte van een gelijkbenige driehoek via de basis en een zijde:

waar a — zijkant van de driehoek, b — basis van de driehoek

Formule voor het berekenen van de oppervlakte van een gelijkbenige driehoek via de basis en een hoek:

waar a — zijkant van de driehoek, b — basis van de driehoek, α — hoek tussen de basis en een zijde.

Formule voor het berekenen van de oppervlakte van een gelijkbenige driehoek via de basis en hoogte:

waar b — basis van de driehoek, h — hoogte, getrokken naar de basis.

Formule voor het berekenen van de oppervlakte van een gelijkbenige driehoek via de zijkanten en de hoek ertussen:

waar a — zijkant van de driehoek, α — hoek tussen de zijkanten.

Formule voor het berekenen van de oppervlakte van een gelijkbenige driehoek via de basis en de hoek tussen de zijkanten:

waar b — basis van de driehoek, α — hoek tussen de zijkanten.

Formule voor het berekenen van de oppervlakte van een gelijkzijdige driehoek via de straal van de omgeschreven cirkel:

waar R — straal van de omgeschreven cirkel.

Formule voor het berekenen van de oppervlakte van een gelijkzijdige driehoek via de straal van de ingeschreven cirkel:

waar r — straal van de ingeschreven cirkel.

Formule voor het berekenen van de oppervlakte van een gelijkzijdige driehoek via een zijde:

waar a — zijde van de driehoek.

Formule voor het berekenen van de oppervlakte van een gelijkzijdige driehoek via de hoogte:

waar h — hoogte van de driehoek.

Type driehoek:

Ongeldige invoer

Berekening via:

Ongeldige invoer

Berekening via:

Ongeldige invoer

Berekening via:

Ongeldige invoer

Berekening via:

Ongeldige invoer

Voer de afmetingen in mm in:

Zijde, a:

Ongeldige invoer

Zijde, b:

Ongeldige invoer

Hoek, a:

Ongeldige invoer

Zijde, a:

Ongeldige invoer

Hoogte, h:

Ongeldige invoer

Zijde, a:

Ongeldige invoer

Hoogte, b:

Ongeldige invoer

Zijde, c:

Ongeldige invoer

Straal van de cirkel, R:

Ongeldige invoer

Zijde, a:

Ongeldige invoer

Hoogte, b:

Ongeldige invoer

Zijde, c:

Ongeldige invoer

Straal van de cirkel, R:

Ongeldige invoer

Zijde, a:

Ongeldige invoer

Hoek, a:

Ongeldige invoer

Hoek, β:

Ongeldige invoer

Zijde, a:

Ongeldige invoer

Hoogte, b:

Ongeldige invoer

Zijde, c:

Ongeldige invoer

Zijde, a:

Ongeldige invoer

Hoogte, b:

Ongeldige invoer

Zijde, c:

Ongeldige invoer

Hoek, a:

Ongeldige invoer

Zijde, a:

Ongeldige invoer

Hoek, a:

Ongeldige invoer

Zijde, c:

Ongeldige invoer

Straal van de cirkel, R:

Ongeldige invoer

Deel, c1:

Ongeldige invoer

Deel, c2:

Ongeldige invoer

Rechthoekszijde, a:

Ongeldige invoer

Rechthoekszijde, b:

Ongeldige invoer

Rechthoekszijde, c:

Ongeldige invoer

Zijde, a:

Ongeldige invoer

Basis, b:

Ongeldige invoer

Zijde, a:

Ongeldige invoer

Basis, b:

Ongeldige invoer

Hoek, a:

Ongeldige invoer

Basis, b:

Ongeldige invoer

Hoogte, h:

Ongeldige invoer

Zijde, a:

Ongeldige invoer

Hoek, a:

Ongeldige invoer

Basis, b:

Ongeldige invoer

Hoek, a:

Ongeldige invoer

Straal, R:

Ongeldige invoer

Straal, r:

Ongeldige invoer

Zijde, a:

Ongeldige invoer

Hoogte, h:

Ongeldige invoer

We tonen het resultaat in:

Ongeldige invoer

Resultaat:

Ongeldige invoer

Informatie

NEN ISO 80000-3 — Standaard voor de wiskundige definitie van geometrische vlakken en formules voor oppervlakteberekeningen, zoals driehoeken en de oppervlakte volgens de formule van Heron.

Weten hoe je de oppervlakte van een driehoek berekent is een fundamenteel concept dat al vroeg op school wordt aangeleerd en blijft van groot belang voor tal van praktische toepassingen. Of je nu een bouwer, ingenieur, technicus of ontwerper bent, het bepalen van de oppervlakte van een rechthoekige driehoek is vaak essentieel bij het plannen van materiaalgebruik of het beoordelen van ontwerpeisen.

Onze driehoek-oppervlakte calculator is ontworpen om meerdere flexibele methoden te bieden voor het berekenen van de oppervlakte van driehoeken—waaronder rechthoekige, gelijkbenige, gelijkzijdige en ongelijkzijdige driehoeken—met verschillende parameters zoals zijden, hoeken of de straal van de omgeschreven cirkel. Deze krachtige tool levert niet alleen direct resultaten, maar toont ook elke rekenstap, waardoor hij ideaal is voor zowel snelle schattingen als een grondige controle van handmatige berekeningen.

Hoe bereken je online de oppervlakte van een driehoek?

Om professionals en liefhebbers efficiënt te helpen bij het beantwoorden van de veelgestelde vraag "Hoe bereken ik de oppervlakte van een driehoek?" en het risico op dure fouten te minimaliseren, hebben wij deze betrouwbare online oplossing ontwikkeld. De calculator past standaard meetkundige formules toe die bij elke combinatie van invoergegevens werken, zodat je de oppervlakte van een gelijkbenige driehoek in slechts enkele seconden uitrekent of moeiteloos de oppervlakte van een gelijkzijdige (ook wel regelmatige) driehoek bepaalt.

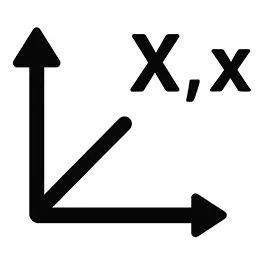
Een driehoek is een fundamentele geometrische figuur gevormd door drie verbonden lijnstukken die samenkomen in hoekpunten. Met onze calculator kun je nauwkeurig de oppervlakte in vierkante meters (m²) bepalen, een belangrijke maat die vooral in de bouw en architectuur van grote waarde is.

Classificatie van driehoeken

Op basis van hoeken:

scherphoekig;
stomphoekig;
rechthoekig.

Op basis van zijden:

gelijkzijdig;
gelijkbenig;
ongelijkzijdig.

Door gebruik te maken van de sinusfunctie en methoden als de formule van Heron, biedt onze driehoek-oppervlakte calculator een krachtige aanpak voor het berekenen van de oppervlakte met zowel drie zijden of met twee zijden en de ingesloten hoek. Deze flexibiliteit zorgt ervoor dat je een breed scala aan driehoeken nauwkeurig en met vertrouwen kunt berekenen.

Deze online calculator minimaliseert het risico op handmatige fouten en bespaart waardevolle tijd door geavanceerde meetkundige en wiskundige principes toe te passen voor snelle en nauwkeurige berekeningen bij elke vorm driehoek.

Oppervlakte driehoek berekenen

Berekenen van de oppervlakte van een driehoek

Informatie

Hoe bereken je online de oppervlakte van een driehoek?

Classificatie van driehoeken

Zie ook: