Inhoud kegel berekenen

Informatie

Wiskunde is de universele taal die ten grondslag ligt aan wetenschap, technologie en bouw. Het speelt een essentiële rol in vakgebieden zoals techniek, architectuur en ontwerp. Vanaf het basisonderwijs maken leerlingen kennis met tal van wiskundige principes en formules, waaronder de fundamentele berekening van de inhoud van een kegel. Zowel rechte (reguliere) kegels als afgeknotte kegels worden routinematig geanalyseerd in professionele bouw- en technische praktijken. Onze online tool – een calculator voor de inhoud van rechte en afgeknotte kegels – biedt snelle, nauwkeurige en betrouwbare berekeningen.

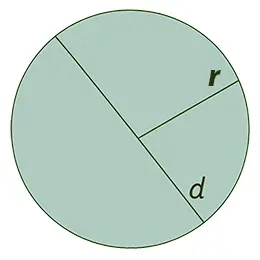
Een kegel is een driedimensionaal geometrisch lichaam dat gevormd wordt door alle stralen vanuit één enkel punt—de top—te verbinden met ieder punt op een vlakke oppervlakte, de basis genoemd. In veel contexten verwijst de term “kegel” specifiek naar het deel van het object dat wordt bepaald door het verbinden van de top met de rand van de basis.

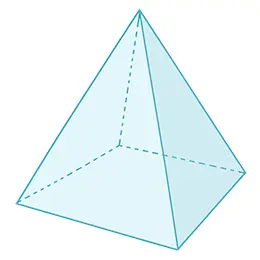
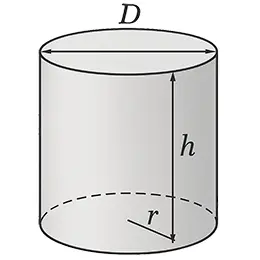
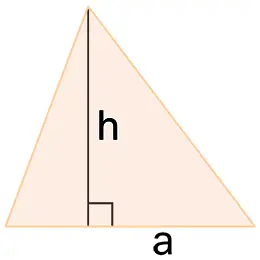
Een loodrechte lijn die van de top naar de basis wordt getrokken, wordt de hoogte van de kegel genoemd. Wanneer de basis een eindige oppervlakte heeft, is de inhoud van de kegel eindig en wordt deze berekend als een derde van het product van het grondvlak en de hoogte. Daarom hebben alle kegels die op gelijke bases rusten met dezelfde hoogte—zelfs als hun toppen in een vlak parallel aan de basis liggen—dezelfde inhoud. Wanneer de basis een veelhoek is, wordt de kegel een piramide, waarmee piramides een specifieke vorm van kegels zijn.

Een lijnstuk dat de top verbindt met een punt op de omtrek van de basis wordt een generator van de kegel genoemd. Deze generatoren samen vormen het zijvlak.

In de bouw en techniek is precisie van het grootste belang. Zelfs een kleine rekenfout kan grote gevolgen hebben. Om zowel nauwkeurigheid als efficiëntie te waarborgen, is onze online tool ontwikkeld om alle relevante kegelformules te berekenen door simpelweg de essentiële waarden in te voeren. Met deze calculator voor de inhoud van rechte en afgeknotte kegels kun je snel de inhoud van een kegel bepalen in kubieke centimeter, kubieke meter of liters.

Er worden drie hoofdformules gebruikt in deze calculator:

1. De formule voor het berekenen van de inhoud van een kegel met behulp van de straal en de hoogte.
2. De formule die de inhoud berekent op basis van het grondvlak en de hoogte.
3. De formule voor het bepalen van de inhoud van een afgeknotte kegel op basis van de straal en hoogte.

Door onze online calculator te gebruiken, profiteer je van:

• Verbeterde nauwkeurigheid en betrouwbaarheid in de berekende resultaten, waardoor potentiële fouten in professionele projecten worden geminimaliseerd.
• Aanzienlijke tijdsbesparing doordat handmatig rekenen overbodig wordt.
• Een intuïtieve en gebruiksvriendelijke interface die eenvoudig te bedienen is.

Om onze online calculator te gebruiken, volg je deze stappen:

• Selecteer het type kegel (recht of afgeknot).
• Voer de benodigde parameters in (hoogte, straal of grondvlak).
• Na het invoeren van de gegevens toont de calculator direct de inhoud van de kegel.