Matematika je univerzální jazyk, který stojí v základu vědy, technologií a stavebnictví. Hraje klíčovou roli v oblastech, jako je inženýrství, architektura a design. Již od základní školy se studenti seznamují s mnoha matematickými principy a vzorci, včetně základního výpočtu objemu kužele. Běžně se v praxi stavebnictví a inženýrství analyzují jak pravé (rovné) kužely, tak i komolé kužely. Náš online nástroj – kalkulačka objemu komolého a pravého kužele – nabízí rychlé, přesné a spolehlivé výpočty.
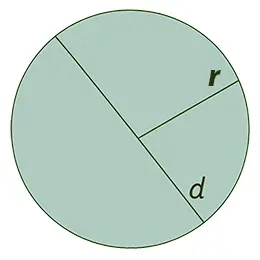
Kužel je trojrozměrné geometrické těleso vzniklé spojením všech polopřímek, které vycházejí z jednoho bodu – vrcholu – a procházejí body rovinné oblasti zvané základna. V mnoha případech se pojmem „kužel“ označuje právě ta část tělesa, která je ohraničena vrcholem a okrajem základny.
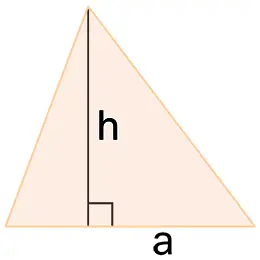
Kolmá úsečka vedená z vrcholu na základnu se nazývá výška kužele. Pokud má základna konečnou plochu, pak je objem kužele konečný a vypočítá se jako jedna třetina součinu plochy základny a výšky. Proto mají všechny kužely s totožnou základnou a stejnou výškou – i pokud jsou jejich vrcholy v rovině rovnoběžné se základnou – stejný objem. Pokud je základna mnohoúhelníkem, není již těleso kužel ale jehlan – proto jehlany patří mezi zvláštní typy kuželů.
Úsečka spojující vrchol s bodem na obvodu základny se nazývá tvořicí kužele. Soubor všech tvořicích vytváří plášť tělesa.
Ve stavebnictví a technických oborech je přesnost naprosto zásadní. I drobná chyba ve výpočtu může mít závažné následky. Aby byla zajištěna maximální přesnost i efektivita, je náš online nástroj konstruován tak, aby umožňoval snadné zadání klíčových hodnot do příslušného vzorce pro výpočet. Pomocí této kalkulačky objemu komolého a rovného kužele rychle získáte výsledek v centimetrech krychlových, metrech krychlových nebo v litrech.
Používání naší online kalkulačky vám přinese tyto výhody:
Postup použití našeho online nástroje: